Application of Moment - Area Method for Simply supported Beams

The deflection δ at some point B of a simply supported beam can be obtained by the following steps:

1. Compute $t_{C/A} = \dfrac{1}{EI}(Area_{AC}) \, \bar{X}_C$ = ZCA

2. Compute $t_{B/A} = \dfrac{1}{EI}(Area_{AB}) \, \bar{X}_B$ = ZBA

3. Slope at support A = O A = t CA /L = ZCA / L

4. Slope at support C = O C = tCA/ L = ZCA / L

5. Solve δ by ratio and proportion (see figure above).

$\dfrac{\delta + t_{B/A}}{x} = \dfrac{t_{C/A}}{L}$

Problem:1

The middle half of the beam shown in Fig. has a moment of inertia 1.5 times that of the rest of the beam. Find the midspan deflection.

(Hint: Convert the M diagram into an M/EI diagram.)

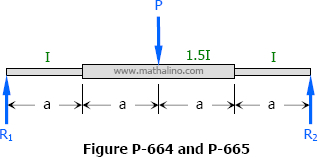
Simple beam with different moment of inertia over the span

Solution :

M/EI diagram of a simple beam with changing moment of inertia

$t_{A/C} = \dfrac{1}{EI}(Area_{AC}) \, \bar{X}_A$

$t_{A/C} = \frac{1}{2}a \left( \dfrac{Pa}{2EI} \right)(\frac{2}{3}a) + a \left( \dfrac{Pa}{3EI} \right)(\frac{3}{2}a) + \frac{1}{2}a \left( \dfrac{2Pa}{3EI} - \dfrac{Pa}{3EI} \right)(\frac{5}{3}a)$

$t_{A/C} = \dfrac{Pa^3}{6EI} + \dfrac{Pa^3}{2EI} + \dfrac{5Pa^3}{18EI}$

$t_{A/C} = \dfrac{17Pa^3}{18EI}$

Therefore,
$\delta_{midspan} = \dfrac{17Pa^3}{18EI} \,\,$ → answer

Problem : 2

Determine the value of EIδ at the right end of the overhanging beam shown in Fig.

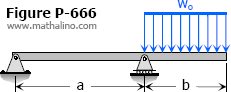
Solution :

$\Sigma M_B = 0$
$aR_A = w_ob(\frac{1}{2}b)$
$R_A = \dfrac{w_ob^2}{2a}$

$EI \, t_{A/B} = (Area_{AB}) \, \bar{X}_A$

$EI \, t_{A/B} = \frac{1}{2}a(\frac{1}{2}w_ob^2)(\frac{2}{3}a)$

$EI \, t_{A/B} = \frac{1}{6}w_oa^2b^2$

$EI \, t_{C/B} = (Area_{BC}) \, \bar{X}_C$

$EI \, t_{C/B} = \frac{1}{3}b(\frac{1}{2}w_ob^2)(\frac{3}{4}b)$

$EI \, t_{C/B} = \frac{1}{8}w_ob^4$

$\dfrac{y_C}{b} = \dfrac{t_{A/B}}{a}$

$y_C = \dfrac{b}{a}t_{A/B}$

$EI \, y_C = \dfrac{b}{a}EI \, t_{A/B}$

$EI \, y_C = \dfrac{b}{a}(\frac{1}{6}w_oa^2b^2)$

$EI \, y_C = \frac{1}{6}w_oab^3$

$\delta_C = y_C + t_{C/B}$

$EI \, \delta_C = EI \, y_C + EI \, t_{C/B}$

$EI \, \delta_C = \frac{1}{6}w_oab^3 + \frac{1}{8}w_ob^4$

$EI \, \delta_C = \frac{1}{24}w_ob^3(4a + 3b) \,\,$ → answer

Comments

Relation between Modulus of Elasticity and Modulus of Rigidity

Modulus of Elasticity (E) It is the ratio between Normal stress to Normal strain within the elastic limit. Elastic Modulus E = Normal stress/Normal strain E = s/e Modulus of Rigidity (G) It is the ratio between Shear stress to Shear strain within the elastic limit. Rigidity Modulus G = Shear stress/ Shear strain G = Ƭ / ø Relation between Modulus of Elasticity and Modulus of Rigidity: Consider a solid cube PQRS is subjected to a shearing force F. Let Ƭ be the shear stress produced in the faces PQ and RS due to this shear force. The complementary shear stress consequently produced in the vertical faces PS and RQ is also equal to same and shown in figure as Ƭ Due to the pure shearing force, the cube is deformed PQRS to PQR'S' . The point S moved to S' and point R moved to R' as shown in fig. The shear strain = The angle of distortion ø ...

Shearing Stresses Distribution in Circular Section

Show that the shearing stress developed at the neutral axis of a beam with circular cross section is τ max = (4/3)(F/πr2). Assume that the shearing stress is uniformly distributed across the neutral axis. Solution : Let us consider the circular section of a beam as displayed in following figure. We have assumed one layer EF at a distance y1 from the neutral axis of the circular section of the beam Shear stress at a section will be given by following formula as mentioned here Where, F = Shear force (N) τ = Shear stress (N/mm2) A = Area of section, where shear stress is to be determined (mm2) ȳ = Distance of C.G of the area, where shear stress is to be determined, from neutral axis of the beam section (m) Q = A. ȳ = Moment of the whole shaded area about the neutral axis I = Moment of inertia of the given section about the neutral axis (mm4) For circular cross-section, Moment of inertia, I = ПR4/4 b = Width of the given section where shear stress is to be determined. Let us co...

PORTAL METHOD and CANTILEVER METHOD

The behavior of a structure subjected to horizontal forces depends on its height to width ratio. The deformation in low-rise structures, where the height is smaller than its width, is characterized predominantly by shear deformations. In high rise building, where height is several times greater than its lateral dimensions, is dominated by bending action. To analyze the structures subjected to horizontal loading we have two methods. Portal method and Cantilever method 1. PORTAL METHOD The portal method is an approximate analysis used for analysing building frames subjected to lateral loads such as Wind loads/ seismic forces. Since shear deformations are dominant in low rise structures, the method makes simplifying assumptions regarding horizontal shear in columns. Each bay of a structure is treated as a portal frame, and horizontal force is distributed equally among them. Assumptions in portal method 1. The points of inflection are located at the mid-height of e...

Prof.Kodali Srinivas

Search This Blog