Buckling of Columns

A structural member loaded axially in compression is generally called a compression member. Vertical compression members in buildings are called columns, posts or stanchions. A compression member in roof trusses is called struts and in a crane is called a boom.
If the load on a column is applied through the center of gravity of its cross section, it is called an 'axial load'. A load at any other point in the cross section is known as an eccentric load. 

As the axial load on a perfectly straight slender column with elastic material properties is increased in magnitude, this ideal column passes through three states:

a)Stable equilibrium :   

The straight column under load is in stable equilibrium if a lateral force, applied between the two ends of the column, produces a small lateral deflection which disappears and the column returns to its straight form when the lateral force is removed.
b)Neutral equilibrium :

If the column load is gradually increased, a condition is reached in which the straight form of equilibrium becomes so-called neutral equilibrium, and a small lateral force will produce a deflection that does not disappear and the column remains in this slightly bent form when the lateral force is removed.
                                             The load at which neutral equilibrium of a column is reached is called the 'Critical load or Buckling load'.
c) Instability :

The state of instability is reached when a slight increase of the column load causes uncontrollably growing lateral deflections leading to complete collapse.

A short column under the action of an axial load will fail by direct compression before it buckles, but a long column loaded in the same manner will fail by buckling (bending), the buckling effect being so large that the effect of the direct load may be neglected. The intermediate-length column will fail by a combination of direct compressive stress and bending.

Euler's buckling load:

In 1757, mathematician Leonhard Euler derived a formula that gives the maximum axial load that a long, slender, ideal column can carry without buckling. An ideal column is one that is perfectly straight, homogeneous, and free from initial stress. The maximum load, sometimes called the critical load, causes the column to be in a state of unstable equilibrium; that is, any increase in the load, or the introduction of the slightest lateral force, will cause the column to fail by buckling. The formula derived by Euler for columns is given below.

The Buckling Load Pcr

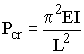The Buckling Strength s_cr is the Euler Buckling Load divided by the column's cross-sectional area A is,

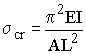where

E = modulus of elasticity,

I = area moment of inertia,

L = unsupported length of column,

The effective length L_e accounts for differences in the end supports. The effective length is the length the column would be if it were to buckle as a pinned-pinned column. The buckling formula for any column is therefore: 

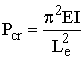Common end-conditions are given here:

Effective Lengths for Columns with Various End Conditions
End Condition	Pinned-Pinned	Fixed-Free	Fixed-Fixed	Fixed-Pinned
The effective length is equal to the distance between points in the column where moment = 0 (between "pins"). This occurs when the curvature of the column changes. The fixed-free column is "mirrored" through the fixed end to visualize Le=2L.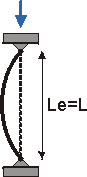
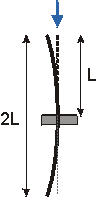
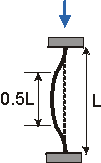
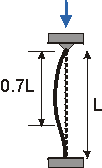
Effective Length, Le	L	2L	0.5L	0.7L
Relative Buckling Strength     (~ 1/ Le2) for same L	1	0.25	4	2

Slenderness ratio:

The ratio of the effective length of a column to the least radius of gyration(r) of its cross section is called the Slenderness ratio . This ratio affords a means of classifying columns. Slenderness ratio is important for design considerations.

Radius of gyration (r) :

It describes the way in which the area of a cross-section is distributed around its centroidal axis. If the area is concentrated far from the centroidal axis it will have a greater value of r and a greater resistance to buckling. A cross-section can have more than one radius of gyration and most sections have at least two. If this is the case, the section tends to buckle around the axis with the smallest value. The radius of gyration is defined as:

I is the Moment of Inertia and A is  the actual cross-section, Distance r is the radius of gyration.

I = Ar²

There generally two bending axes to consider, and thus two radii of gyration:

where

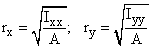
r = radius of gyration I = moment of inertia A = area of the cross section

Note : All things being equal, a circular pipe is the most efficient column section to resist buckling. This is because it has an equal radius of gyration in all directions and it has the its area distributed as far away as possible from the centroid.

Rankine's formula 

It is one of the most widely known formulae for the design and investigation of columns employed in engineering practice.

Let,

A = Cross-sectional area of the  column ,

L = Effective length of the column,

σc = Compressive yield stress,

WB = Buckling load,

Ixx and Iyy = Moment of inertia of the section about X-axis and Y-axis respectively, 

kxx and kyy = Radius of gyration of the section about X-axis and Y-axis respectively. The minimum radius of gyration will be consider for calculating the buckling load. 

According to Rankine’s formula, 

Where a is Rankin's Constant

The value of this constant for  mild steel is 1 / 7500, 

for wrought iron 1 / 9000, and  1 / 1600, for cast iron