Skip to main content

Dynamics - Key Concepts



In Engineering Mechanics  the study of the causes of motion and changes in motion is called as Dynamics. 

For convenience, dynamics is divided into two branches, Kinematics and Kinetics.

Kinematics :It is the branch of classical mechanics that describes the motion of bodies (objects) and systems (groups of objects) without consideration of the forces that cause the motion.

Kinetics:It is the branch of classical mechanics that describes the motion of bodies (objects) and systems (groups of objects) by consideration of the forces that cause the motion.

Types of Motion:

There are three types of motion,
  • Translatory motion
  • Rotatory motion
  • Vibratory motion
Translatory motion:
In translatory  motion the particle moves from one point in space to another. This motion may be along a straight line or along a curved path.
Motion of a particle along a straight line is called Rectilinear motion and 
Motion along a curved path is called Curvilinear motion.
Curvilinear motion:
A car moving on a curved road.
Rectilinear motion :
A car moving  in a straight road 
Rotatory motion:
In rotatory motion the particles of the body describe concentric circles about the axis of motion.
Rotatory motion: rotating Top


Vibratory motion:
In vibratory motion the particles move to and fro about a fixed point.
Vibratory motion: Simple Pendulum
Distance and Displacement:
Distance and displacement are two quantities that may seem to mean the same thing yet have distinctly different definitions and meanings.
Displacement is a vector quantity, that refers to  the object's overall change in position.Displacement is a measurement of change in position of the particle in motion. Its magnitude and direction are measured by the length and direction of the straight line joining initial and final positions of the particle. Obviously, the length of the straight line between the positions is the shortest distance between the points.

Distance is a scalar quantity that refers to "how much ground an object has covered" during its motion.

Speed and Velocity:



Speed is the rate of change of distance with time, and Velocity is the rate of change of displacement with time.Speed is the first derivative of distance with respect to time,and Velocity is the first derivative of displacement with respect to time.
The average speed during the course of a motion is often computed using the following formula:
In contrast, the average velocity is often computed using this formula

Acceleration:
It is the rate of change of velocity with respect to time. 
The term acceleration is used in general for an increase the magnitude of velocity wiht respect to time. a decrease in velocity is called deceleration.
Acceleration shows the change in velocity in a unit time. Velocity is measured in meters per second, m/s, so acceleration is measured in (m/s)/s, or m/s2, which can be both positive and negative.

Uniform acceleration

Uniform or constant acceleration is a type of motion in which the velocity of an object changes by an equal amount in every equal time period.
simple formulae that relate the following quantities: displacement, initial velocity, final velocity, acceleration, and time:
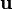\mathbf {v}= \mathbf {u} + \mathbf {a} t
\mathbf {s}= \mathbf {u} t+ {{1} \over {2}} \mathbf {a}t^2 = {{(\mathbf{u}+\mathbf{v})t} \over {2}}
|\mathbf {v}|^2= |\mathbf {u}|^2 + 2 \, \mathbf {a} \cdot \mathbf {s}
where
\mathbf{s} = displacement
\mathbf{u} = initial velocity
\mathbf{v} = final velocity
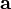\mathbf{a} = uniform acceleration
t = time.

Motion with Variable acceleration
The equations derived for uniformly accelerated motion are not applicable to the motion with variable acceleration. 
The relation between,

displacement, initial velocity, final velocity, acceleration, and time are,


Instantaneous velocity
 
Instantaneous acceleration
a = v. dv/dx
 Relation between acceleration and velocity
Kinematic equation for motion
 
when one or more of the above quantities are specified, the other can be obtained by process of differentiation or integration, using the above relationships.
In problems requiring integration, the constants of integrations can be determined from specified conditions of motion.

EXAMPLE
: 

If the position of a particle along x – axis varies in time as :

x=2t2−3t+1
Then :
  1. What is the velocity at t = 0 ?
  2. When does velocity become zero?
  3. What is the velocity at the origin ?
Solution : 
We first need to find out an expression for velocity by differentiating the given function of position with respect to time as :
v=đđt(2t2−3t+1)=4t−3
(i) The velocity at t = 0,
v=4x0−3=−3m/s
(ii) When velocity becomes zero :
For v = 0,
4t−3=0⇒t=34=0.75 s.
(iii) The velocity at the origin :
At origin, x = 0,
x=2t2−3t+1=0⇒2t2−2t−t+1=0⇒2t(t−1)−(t−1)=0⇒t=0.5 s, 1 s.
This means that particle is twice at the origin at t = 0.5 s and t = 1 s. Now,
v(t=0.5 s)=4t-3=4x0.5−3=-1 m/s.
Negative sign indicates that velocity is directed in the negative x – direction.
v(t=1 s)=4t-3=4x1−3=1 m/s.
Labels:

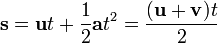
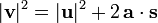
Comments

Post a Comment

Popular posts from this blog

Relation between Modulus of Elasticity and Modulus of Rigidity

Modulus of Elasticity (E)   It is the ratio between Normal stress to Normal strain within the elastic limit. Elastic Modulus E = Normal stress/Normal strain E =  s/e Modulus of Rigidity (G)  It is the ratio between Shear stress to Shear strain within the elastic limit. Rigidity Modulus G = Shear stress/ Shear strain G =    Ƭ / ø   Relation between Modulus of Elasticity and Modulus of Rigidity: Consider a solid cube  PQRS is  subjected to a shearing force F.  Let  Ƭ     be the shear stress produced in the faces PQ and RS due to this shear force. The complementary shear stress consequently produced in the vertical faces PS and RQ is also equal to same and shown in figure as Ƭ   Due to the pure shearing force, the cube is deformed PQRS to PQR'S' . The point   S moved to S' and point R moved to R' as shown in fig.  The shear strain = The angle of distortion  ø           ...
5 comments
Read more

Shearing Stresses Distribution in Circular Section

Show that the shearing stress developed at the neutral axis of a beam with circular cross section is  τ max = (4/3)(F/πr2). Assume that the shearing stress is uniformly distributed across the neutral axis.  Solution : Let us consider the circular section of a beam as displayed in following figure. We have assumed one layer EF at a distance y1 from the neutral axis of the circular section of the beam Shear stress at a section will be given by following formula as mentioned here Where, F = Shear force (N) τ = Shear stress (N/mm2) A = Area of section, where shear stress is to be determined (mm2) ȳ = Distance of C.G of the area, where shear stress is to be determined, from neutral axis of the beam section (m) Q = A. ȳ = Moment of the whole shaded area about the neutral axis I = Moment of inertia of the given section about the neutral axis (mm4) For circular cross-section, Moment of inertia, I = ПR4/4 b = Width of the given section where shear stress is to be determined. Let us co...
1 comment
Read more

PORTAL METHOD and CANTILEVER METHOD

The behavior of a structure subjected to horizontal forces depends on its height to width ratio. The deformation in low-rise structures, where the height is smaller than its width, is characterized predominantly by shear deformations. In high rise building, where height is several times greater than its lateral dimensions, is dominated by bending action. To analyze the structures subjected to horizontal loading we have two methods. Portal method  and Cantilever method 1. PORTAL METHOD The portal method is an approximate analysis used for analysing building frames subjected to lateral loads such as Wind loads/ seismic forces.  Since shear deformations are dominant in low rise structures, the method makes simplifying assumptions regarding horizontal shear in columns.  Each bay of a structure is treated as a portal frame, and horizontal force is distributed equally among them. Assumptions in portal method   1. The points of inflection are located at the mid-height of e...
3 comments
Read more