Elastic Section Modulus

According to Theory of bending,within the elastic limit, the bending stress (f) is directly proportional to the distance y from the neutral axis.

The maximum value of bending stress (fmax) will be the outermost fiber ie,y = ymax

                               fmax = [M/I]. ymax

We can write this equation as,

fmax = [M/Z]

Where Z = I/ymax

and Z is called as Elastic Section Modulus.

The stress in the outermost section of beam is computed with the help of section modulus (Z).

Section Modulus

It is a ratio between second moment of area (area Moment of Inertia) and distance from Neutral axis to the extreme fiber. 

Section modulus, Z = I/ymax

Where,

I   = Moment of inertia about Neutral axis (N.A.) 

ymax =The maximum distance of the fiber from N.A

Note:

1.Section modulus is also expressed as the ratio of bending moment (M) to the bending stress(fmax) of a given object within the elastic limit.

Section modulus, Z = M/fmax 

2.Section modulus also represent the measure of strength of given member. More the section modulus, more the member is resistant to bending of the beam.

Elastic Section modulus of symmetrical sections:

1.Section modulus (Z) of a solid Rectangular section of breadth b and depth d

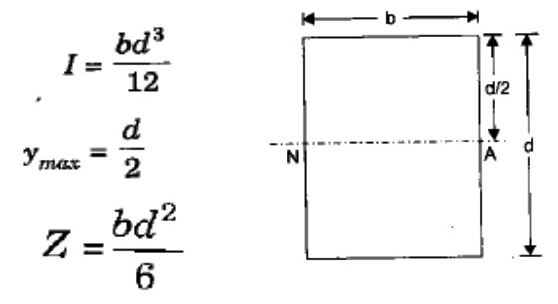
2.Section modulus (Z) of Hollow Rectangular cross section of outer and inner breadth B,b and depth D,d as shown in figure.

3.Section modulus (Z) of a solid circular cross section of diameter d

4.Section modulus (Z) of a Hollow circular cross section of outer diameter D and internal diameter d