 |
| Jean le Rond d’Alembert |
This principle, is alternative form of Newton’s second law of motion, stated by the 18th-century French polymath Jean le Rond d’Alembert.
In effect, the principle reduces a problem in dynamics to a problem in statics.
The Newton's second law states that the force F acting on a body is equal to the product of the mass m and acceleration a of the body, or
F = ma
F = ma
The above equation will be re write in D’Alembert’s form is
F - ma = 0
In other words, the body is in equilibrium under the action of the real force 'F' and
the fictitious force ( -ma).
the fictitious force ( -ma).
The fictitious force is also called an 'inertial force' and a reversed effective force.


 The Radius of curvature of the curve is defined as the radius of the approximating circle. This radius changes as we move along the curve.
The Radius of curvature of the curve is defined as the radius of the approximating circle. This radius changes as we move along the curve.
The formula for the radius of curvature at any point x for the curve
y = f(x) is given by:

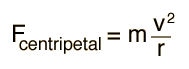
Centrifugal force:
Centrifugal force is
a fictitious or inertial force and it
represents the effects of inertia that arise in connection with rotation and which are experienced as an outward force away from the center of rotation and equal to centripetal force.
It is defined as the force that tends to make rotating bodies move away from the center of rotation.
Rotation of Rigid Body about Fixed axis

Equations for constant angular acceleration

The Linear acceleration here is the tangential acceleration. The relation between angular velocity and radius of path with tangential acceleration at is,

In addition to any tangential acceleration, there is always the centripetal acceleration:

Acceleration of a Body in Curvilinear Motion

Components of total acceleration in normal and tangential directions (t - n axis)
The tangential acceleration, tangent to trajectory and parallel to velocity is,
The centripetal acceleration, or normal acceleration to trajectory and directed to its center is,
Where,R is Radius of curvature of trajectory at time 
The formula for the radius of curvature at any point x for the curve
y = f(x) is given by:
The Magnitude of total acceleration,
Centripetal Force:
Any motion in a curved path represents accelerated motion, and requires a force directed towards the center of curvature of the path. This force is called the centripetal force which means "center seeking" force.
Any motion in a curved path represents accelerated motion, and requires a force directed towards the center of curvature of the path. This force is called the centripetal force which means "center seeking" force.
The force has the magnitude, Fc = m an
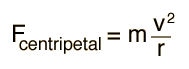

Rotation is described in terms of angular displacement , time , angular velocity, and angular acceleration . Angular velocity is the rate of change of angular displacement and angular acceleration is the rate of change of angular velocity.
The averages of velocity and acceleration are defined by the relationships:
|
| Average angular acceleration: |  |


In addition to any tangential acceleration, there is always the centripetal acceleration:



Comments
Post a Comment