Skip to main content

Principal Stresses

Principal Plane and Principal Stress

It is the Plane in which only normal stress is acting without Shear Stresses is called principal plane.
The normal stresses which are acting on Principal Plane are called as Principal Stress.

Sign Conventions:



1.Tensile normal stress is considered as positive and compressive normal stress is considered as negative.
2. Shear stress acting on a face is considered positive if it rotate the element in clockwise direction and negative if in anticlockwise direction.

Stresses on Oblique Plane



The normal stresses (sx and sy) and the shear stress (txy) are acting vary smoothly on a body, the normal and tangential stresses or shear stress acting on a Oblique plane making a rotation of an angle q  to the vertical face are given by,
Normal stress on inclined plane  
sq = (sx+sy)/2 + {(sx-sy)/2}cos2q + txy sin2q                                                                       -- (1)
Shear stress in the inclined plane
      tq = {(sx-sy)/2} sin2q  -  txy cos2q - (2)

In above equations, there exist a couple of particular angles where the stresses take on special values.
First, there exists an angle qp witch is called principal plane , here the shear stress txy becomes zero. 
That angle qp is found by setting txy to zero in the above shear transformation equation. The result is, the principal planes are located at 
                      ----(3) 
This equation will express in a triangle and calculate cos2q , Sin2q
                           
by substitute the cos2q , Sin2q in stress transformation equation (1) and principal stresses are found from the original stresses (expressed in the x,y directions) via,

The Maximum and Minimum principal stresses are
We can express principal stresses in single equation ---(4)
solving the above equation(3) for qp  we have a set of two values for qp The angle qp defines the principal directions where the only stresses are normal stresses. These stresses are called principal stresses.
These two values will be separated by 90 degree (or, 2qp will be separated by 180 degree). One angle will correspond to the maximum normal stress,and the other will correspond to the minimum normal stress.
The transformation to the principal directions can be illustrated as shown in a figure.



Maximum Shear Stress and Direction:

Another important angle, qs, is where the maximum shear stress occurs. This is found by finding the maximum shear stress by differentiate the shear transformation equation and equate to zero. 
The result is, 
By substituting (cos2q , Sin2q) in  shear stress transformation equation (2),The maximum shear stresses are found from the original stresses (expressed in the x,y directions). 
Maximum Shear stress  ( max) on plane is given by
Maximum Shear stress (max) may also express in terms of principal stressess. 
t max = (s1 - s2) / 2

The maximum shear stress is equal to one-half the difference between the two principal stresses, 
The maximum shear stress plane qs is 45 degrees from principal plane qp.
qs  = qp + 45
The transformation to the maximum shear stress direction can be illustrated as:



Transformation of stresses in two dimensions,showing the planes of action of principal stresses, and maximum and minimum shear stresses are shown in the above figure.

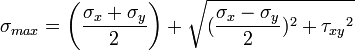
Example:

For a given loading conditions the state of stress in the wall of a cylinder is subjected to normal stresses 85 MN/m2 tensile,in x- direction and  25 MN/m2 tensile in y- direction,along with  Shear stresses of 60 MN/m2 on the planes on which the stresses are act.  the sheer couple acting on planes carrying the 25 MN/m2 stress is clockwise.
a)Calculate the principal stresses and the planes on which they act. 
b)What would be the effect on these results if owing to a change of loading if the 85MN/m2 becomes compressive while other stresses are remain unchanged.

Solution:

The given data 
sx = 85 MN/m2  (ten)
sy  = 25 MN/m2 (ten)
txy = 60 MN/m2(clockwise)
substitute this values in corresponding equations, we get ans. 



a)The principle stresses are given by the formula
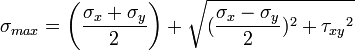
                 \begin{align} \sigma_{max} &= \left(\frac{\sigma_x + \sigma_y}{2} \right )+\sqrt{(\frac{\sigma_x- \sigma_y}{2})^2+ {\tau_{xy}}^2} \end{align}

For finding out the planes on which the principal stresses act us the equation
 Tan ø = 2 xy / x - y
                                                          
The solution of this equation will yield two values q i.e they q1 and q2 giving,    
                  q1= 31.71' and q2= 121.71'
(b) In this case only the loading (a) is changed i.e. its direction had been changed. While the other stresses remains unchanged hence now the block diagram becomes.
Again the principal stresses would be given by the equation.
q1= -23.74 and q2= 113.74

Labels:

Comments

Post a Comment

Popular posts from this blog

Relation between Modulus of Elasticity and Modulus of Rigidity

Modulus of Elasticity (E)   It is the ratio between Normal stress to Normal strain within the elastic limit. Elastic Modulus E = Normal stress/Normal strain E =  s/e Modulus of Rigidity (G)  It is the ratio between Shear stress to Shear strain within the elastic limit. Rigidity Modulus G = Shear stress/ Shear strain G =    Ƭ / ø   Relation between Modulus of Elasticity and Modulus of Rigidity: Consider a solid cube  PQRS is  subjected to a shearing force F.  Let  Ƭ     be the shear stress produced in the faces PQ and RS due to this shear force. The complementary shear stress consequently produced in the vertical faces PS and RQ is also equal to same and shown in figure as Ƭ   Due to the pure shearing force, the cube is deformed PQRS to PQR'S' . The point   S moved to S' and point R moved to R' as shown in fig.  The shear strain = The angle of distortion  ø           ...
5 comments
Read more

Shearing Stresses Distribution in Circular Section

Show that the shearing stress developed at the neutral axis of a beam with circular cross section is  τ max = (4/3)(F/πr2). Assume that the shearing stress is uniformly distributed across the neutral axis.  Solution : Let us consider the circular section of a beam as displayed in following figure. We have assumed one layer EF at a distance y1 from the neutral axis of the circular section of the beam Shear stress at a section will be given by following formula as mentioned here Where, F = Shear force (N) τ = Shear stress (N/mm2) A = Area of section, where shear stress is to be determined (mm2) ȳ = Distance of C.G of the area, where shear stress is to be determined, from neutral axis of the beam section (m) Q = A. ȳ = Moment of the whole shaded area about the neutral axis I = Moment of inertia of the given section about the neutral axis (mm4) For circular cross-section, Moment of inertia, I = ПR4/4 b = Width of the given section where shear stress is to be determined. Let us co...
1 comment
Read more

PORTAL METHOD and CANTILEVER METHOD

The behavior of a structure subjected to horizontal forces depends on its height to width ratio. The deformation in low-rise structures, where the height is smaller than its width, is characterized predominantly by shear deformations. In high rise building, where height is several times greater than its lateral dimensions, is dominated by bending action. To analyze the structures subjected to horizontal loading we have two methods. Portal method  and Cantilever method 1. PORTAL METHOD The portal method is an approximate analysis used for analysing building frames subjected to lateral loads such as Wind loads/ seismic forces.  Since shear deformations are dominant in low rise structures, the method makes simplifying assumptions regarding horizontal shear in columns.  Each bay of a structure is treated as a portal frame, and horizontal force is distributed equally among them. Assumptions in portal method   1. The points of inflection are located at the mid-height of e...
3 comments
Read more