Failure theories

When a component is subject to increasing loads it eventually fails. It is comparatively easy to determine the point of failure of a component subject to a single tensile force. The strength data on the material identifies this strength. However when the material is subject to a number of loads in different directions some of which are tensile/compressive  and some of which are shear, then the determination of the point of failure is more complicated.

Metals can be broadly separated into 'Ductile' metals and 'Brittle' metals. Examples of ductile metals include mild steel, copper etc . Cast iron is a typical brittle metal.Ductile metals under high stress levels initially deform plastically at a definite yield point or progressively yield. In the latter case a artificial value of yielding past the elastic limit is selected in lieu of the yield point e.g 2%proof stress. 

At failure a ductile metal will have experienced a significant degree of elongation. Brittle metals experience little ultimate elongation prior to failure and failure is generally sudden.

A ductile metal is considered to have failed when it has suffered elastic failure, that is when a marked plastic deformation has begun. 

There are five important failure theories, namely 

(1) Maximum Principal stress theory

(2) Maximum Principal Strain theory

(3) Maximum shear stress theory, 

(4) Maximum strain energy theory, and 

(5) Maximum distortion energy theory.

1.The maximum principal stress theory :

The theory also called as Rankine stress theory.This theory is approximately correct for cast iron and brittle materials generally.

According to this theory failure will occur when the maximum principal stress (tensile or compressive) in a system reaches the value of the maximum strength at elastic limit in simple tension.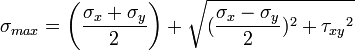                     

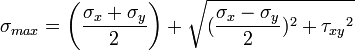
Failure is predicted in this theory when either of the principal stresses(σ1 or σ2 ) is equqls or exceeds the yield stress σy of the material.

 σ₁ = σ_{y   OR}   σ₂  = σ_y

The design Factor of Safety 'n' for two dimensional stress case is, 
Facor of safety  n =σ_y/σ₁ 
n = Elastic Limit stress in tensile test / highest principal stress

2.Maximum Principal Strain theory 

It is also called St. Venant's theory. Yielding will occur when the maximum principal strain just exceeds the strain at the tensile yield point in either simple tension or compression.

e1, e2 are maximum and minimum principal strains corresponding normal stresses σ1 and σ2, then

3.The Maximum Shear Stress Theory :

The theory associated with Tresca and Guest.This is very relevant to ductile metals. It is conservative and relatively easy to apply.

According to this theory, that failure occurs when a maximum shear stress attains a certain value. This value being the value of shear strength at failure in the tensile test. 

In this instance it is appropriate to choose the yield point as practical failure. If the yield point = σy and this is obtained from a tensile test and thus is the sole principal stress then,

the maximum shear stress txy is easily identified as σy /2 . 

txy = σy /2

In the context of a complicated stress system the initial step would be to determine the principle stress i.e. σ1, σ1 and σ3-

then the maximum shear stress would be determined 

The Maximum Shear Stress tmax  will be Greatest of 

 ( σ1 - σ2 ) / 2 or  ( σ2 - σ3 ) / 2  or ( σ1 - σ3 ) / 2

The factor of safety selected would be

n = σy / ( 2 . t max ) = σy / ( σ1 - σ3 )

4.Strain Energy Theory :

The theory associated with Haigh.

This theory is based on the assumption that strains are recoverable up to the elastic limit, and the energy absorbed by the material at failure up to this point is a single valued function independent of the stress system causing it. 

The strain energy per unit volume causing failure is equal to the strain energy at the elastic limit in simple tension.

The following relationship can be derived from this theory.

σy - is the yield point in simple shear and

ν = poisson's ratio. 

Failure Occurs with this theory when,

(σ₁) ² + (σ₂) ² + (σ₃ ) ² -  2v.(σ₁.σ₂ + σ₂.σ₃ + σ₁.σ₃ )     ≥   (σy) ²

5.Distortion Energy Theory 

Also called Shear Strain Energy Theory

This theory is also known as the Von Mises-Hencky theory. Detailed studies have indicated that yielding is related to the shear energy rather than the maximum shear stress..

Strain energy is energy stored in the material due to elastic deformation. The energy of strain is similar to the energy stored in a spring. Upon close examination, the strain energy is seen to be of two kinds : one part results from changes in mutually perpendicular dimensions , and hence in volume, with no change angular changes: the other arises from angular distortion without volume change. The latter is termed as the shear strain energy , which has been shown to be a primary cause of elastic failure..

Failure is predicted when the distortional energy associated with the principal stresses, σ1,2,3 equals or exceeds the distortional energy corresponding to that for the yield strength, σy, of the material in uniaxial tension or compression.

(σ1 - σ2) 2 + (σ2 - σ3) 2 + (σ1 - σ3 ) 2 = 2 σy2

Comparison of Theories:

1.Out of these five theories of failure, the maximum principal stress theory,maximum principal strain theory and strain energy theories are only applicable for brittle materials.

2.The maximum shear stress theory and distortion energy theory are applicable for ductile materials. Out of these two, the distortion energy theory provides most accurate results in majority of the stress conditions.

3.The strain energy theory needs the value of Poisson’s ratio of the part material, which is often not readily available.

4.The maximum shear stress theory is conservative. 

5.For simple unidirectional normal stresses all theories are equivalent, which means all theories will give the same result.