Principal stresses - Mohr's Circle of stresses

Mohr's circle is a graphical representation of a general state of stress at a point. It is a graphical method used for evaluation of principal stresses, maximum shear stress for a given normal and tangential stresses on any given plane.

This method invented by German civil Engineer  Otto Mohr in 1882. It is extremely useful because it enables you to visualize the relationships between the normal and shear stresses acting on various inclined planes at a point in a stressed body.

Mohr's Circle for Plane Stress 

To establish Mohr's Circle, we first recall the stress transformation equations for plane stress at a given location,

sq = (sx+sy) /2 + (sx-sy) /2cos2q +txysin2q - - (1)

tq = (sx-sy)/2sin2q - txycos2q -- (2)

Adding the two  equations (1) and (2) after squaring the equations and Using a basic trigonometric relation we have,

                        (sq- save)2  + t2q= R2
  W here 

                              save = (sx + sy) / 2

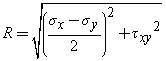
This is the equation of a circle, plotted on a graph where the abscissa is the normal stress and the ordinate is the shear stress.

This circle is with radius of 'R' and centered at point C (save, 0) as shown in the Fig. below,

Following important points must be noted for graphical analysis by Mohr's circle:

Sign convention 

1. The normal stresses are plotted along the horizontal axis (σ-axis) with a sign convention. The tensile stresses are considered positive and compressive stresses are considered negative. 

2. The Shear stresses are plotted in vertical axis (t) with the sign convention given. Shear stress which causes clockwise rotation of element is considered positive while other one which causes anticlockwise rotation is considered negative.

Construction of Mohr’s circle

1. Identify the stresses on the element σx, σy, and txy with the proper sign.

2. Draw a set of σ - t coordinate axes with σ being positive to the right and t being positive in the upward direction.

3. Choose an appropriate scale for the each axis and plot the stresses (σx, -txy) on the x face of the element in this coordinate system (point X). Repeat the process for the y face stresses (σy, txy) and mark the point Y .

4. Draw a line between the two point X and Y. The point where this XY line crosses the σ axis establishes the center of the circle C. 

5. Draw the complete circle with a radius of Rm= CX or CY .

6. For angle measurements (i.e. θ) we consider the line from the center of the circle CX (the reference axis,θ is zero) to corresponding axis (θ) 

7.The two end points of the horizontal diameter are principal stresses, σ1 and σ2 are shown by the points A and B (along the horizontal axis where txy = 0). The rotation angle to the principal axis is θp which is 1/2 the angle from the line CX to the horizontal line OAB. 

The point σ1 represents the maximum normal stress (σmax) and the point σ2 is the minimum normal stress (σmin).
Note: The angle between the reference axis CX and the σ - axis is equal to 2θp.

8. The maximum shear stress is defined by the points H and H’ which are the end points of the vertical diameter line.
The maximum shear stress is equal to the radius of the circle 
(the diameter of circle = max principal stress - min principal stress) 
The line is orthogonal to the principal stress line and thus the maximum shear stress acts along a plane 45° (2θ = 90°) from the principal stress system. 

9.The Coordinates of various points on Mohr's circle represent the state of stress at different planes.The radius of circle to any point on it's circumference represents the axis directed normal to the plane whose stress components are given by the coordinates of that point. 

10.The angle between radii to points on Mohr's circle is twice the angle between the normals to the actual planes represented by these points. The rotational sense of this angle is same as that of rotational sense of the actual angle between the normal to the plane.